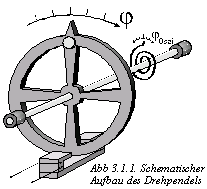
3.2 Versuchsdurchführung
Der oben beschriebene Versuch wurde an einem Drehpendel der Ludwig-Maximilians- Universität durchgeführt. Dabei wurde deutlich, daß die Anregungsfrequenz in der Nähe bzw. etwas unter der Eigenschwingfrequenz des Pendels liegen muß, damit es zu einer Resonanz und damit zu einem chaotischen Verhalten des Pendels kommt.Die aktuelle Auslenkung und die Geschwindigkeit des Pendels wurden während des Versuchs gemessen und zur Auswertung an einen Computer weitergeleitet, der u.a. ein Auslenkungs/Zeit (j/t) - und ein Winkelgeschwindigkeit/Auslenkungs (w/j) - Diagramm ausdrucken konnte (siehe Abbildung 3.2.1, die direkt aus dem Drehpendelversuch stammt. Die Masse der Unwucht betrug dabei 100g). [Tut mir leid wegen der komischen Buchstaben; das j sollte eigentlich ein phi sein und das w ein omega].
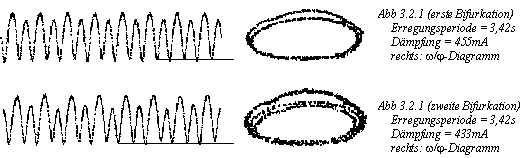
Vergleicht man diese Abbildung mit denen aus der Simulation (vgl. 4.1), so
kann man eine Ähnlichkeit feststellen. In 4.1 wird auch die Bifurkation
(Aufspaltung einer Schwingung) näher erklärt.
Schaltet man den Oszillator und die Wirbelstrombremse aus (jMax Oszi = I =
0), so ergibt sich für das neue Drehmoment M:
M = -DĚj + mgrĚsin(j). Dadurch läßt
sich das Potential U des Pendels im Winkel j berechnen:
Wird das Pendel nicht angeregt (jMax Oszi = 0), verliert es zunehmend an
Energie und pendelt sich schließlich in der Ruhelage jRuhe ein. In der
Ruhelage ist das Drehmoment M = 0, d.h. das Rückstellungsmoment der
Feder ist gleich dem Drehmoment der Masse:
Wird die Unwucht weggelassen (m = 0), so ergibt sich folgendes Drehmoment:
Verstärkt man die Wirbelstrombremse (durch einen relativ großen
Dämpfungstrom), so stellt sich eine periodische Schwingung um die
Ruhelage jRuhe ein. Das Pendel ist dort in Resonanz.
Zurück zum letzten Kapitel ("Das Magnetpendel")
3.3 Theoretische Grundlagen der Simulation
[Dieser Punkt wurde hier weggelassen, weil er voll mit Formeln ist, die HTML
nicht darstellen kann. Wer sich dennoch dafür interessiert, der kann mir
gerne eine e-mail schicken.]
3.4 Optimierung der Formeln für die Simulation
[Dieser Punkt wurde hier weggelassen, weil er voll mit Formeln ist, die HTML
nicht darstellen kann. Wer sich dennoch dafür interessiert, der kann mir
gerne eine e-mail schicken.]
3.5 Weitere Beobachtungen
(3.5.1) 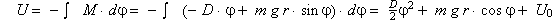
(3.5.2) 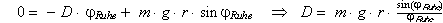
Bei gegebenem jRuhe läßt sich somit die Federkonstante
berechnen (sofern m, g, und r ebenfalls gegeben)
(3.5.3) 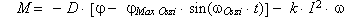
In diesem Fall pendelt das Pendel so lange, bis die zugeführte
Energie (durch den Oszillator) gleich der abgegebenen Energie (durch die
Reibung) ist. Es stellt sich eine harmonische Schwingung ein, die die
folgende Differentialgleichung hat:
(3.5.4) 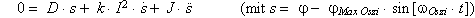
3.6 Anleitung zu den Simulationsprogrammen für das Drehpendel
[Auch diesen Abschnitt habe ich weggelassen. Wer sich dennoch dafür
interessier (Programm oder Beschreibung), kann mir ja mal eine
e-mail schreiben...]
Weiter mit dem nächsten Kapitel ("Chaotische Phänomene am Beispiel des Drehpendels")
(C) Copyright 1997 by Johannes Schmid
letzte Änderung: 05. Januar 1997