Vorbem.
Magnetpend.
Drehpend.
Phänomene
Literatur
2. Das Magnetpendel
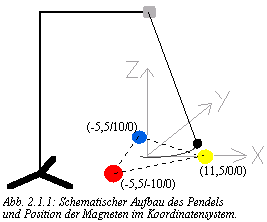
2.1 Versuchsaufbau
Drei mit verschiedenen Farben (rot, gelb und blau) gekennzeichnete, gleich große und gleich starke Magneten werden so auf eine Ebene gestellt, daß sie die Ecken eines gleichseitigen Dreiecks mit der Seitenlänge 20 cm bilden. Über den Schwerpunkt dieses Dreiecks wird ein Pendel (ein Faden von etwa 1,5 m Länge, an dem eine mit Graphit bedampfte Styroporkugel mit einem Durchmesser von etwa 3 cm befestigt ist) gehängt, so daß es die Magneten knapp nicht mehr berührt. Die Kugel pendelt unter dem Einfluß der Anziehungskraft der drei Magneten. (Abb. 2.1.1)Die oben gegebenen Maße sind nur Beispiele und lassen sich beliebig
ändern. Die Magneten sollten jedoch immer stärker als die
Schwerkraft sein, um das Pendel aus dem Schwerpunkt des Dreiecks, dem
natürlichen Ruhepunkt des Pendels, herauszuziehen.
Aber über welchem? Neben den durch die Anordnung bestimmten
Konstanten ist die Startposition die einzige Größe, die auf das
Ergebnis Einfluß nimmt. Ein Magnet zieht das Pendel dann an sich, wenn
es in seiner unmittelbaren Umgebung gestartet wird. Andernfalls kann das
Pendel jedoch auch über einem Magneten stehenbleiben, der von der
Startposition weit entfernt ist. Ist letzteres der Fall, ist also nur eine
Anfangsposition gegeben, die nicht im direkten Einflußgebiet des
Magneten liegt, so lassen sich über die Bahn, die das Pendel beschreibt
-und damit auch über dessen Endposition- keine Vorhersagen treffen.
Um dieses Phänomen näher zu untersuchen, wird der Startpunkt
(also die Position des Pendels beim Loslassen) dem Endpunkt (der Magnet, an
dem das Pendel am Schluß "hängenbleibt")
gegenübergestellt. Dies geschieht in Form einer Karte, auf der der
Startpunkt mit der Farbe des Magneten gefärbt wird, über dem das
Pendel letztendlich stehen bleibt. Ein Pendel, das über einem roten
Gebiet der Karte, dem Attraktionsgebiet des roten Magneten, gestartet wird,
bleibt demnach schließlich über dem roten Magneten stehen.
Zeichnet man mehrere Karten (mit den gleichen Magneten und
Naturkonstanten), so wird man feststellen, daß sie sich voneinander
unterscheiden, obwohl der durchgeführte Versuch jedesmal der gleiche
ist. Eindeutige Gebiete wie die um die Magneten selbst werden sich nicht
ändern, da in diesem Fall das Pendel sofort am Magnet hängenbleibt,
aber der "Rest" wird sich voneinander unterscheiden. Dies liegt
daran, daß man nie zweimal genau denselben Startpunkt treffen kann.
Auch wenn der Unterschied zwischen den Anfangspunkten noch so gering ist, so
vergrößert sich die Differenz zwischen den Pendelbahnen im Verlauf
des Experiments so stark, daß sie nachher so groß ist wie die
Meßwerte selbst.
Die Auswertung ist jedoch mit den Mitteln des Experiments nur
äußerst mühsam zu erfassen. Hier hilft die Computersimulation.
Dieser Abschnitt beschäftigt sich deshalb mit den Auswirkungen der
Veränderung der Reibung. Verkleinert man beispielsweise die
Reibungskonstante µ, so verliert das Pendel erst später seine Energie;
es pendelt also länger. Dadurch wird der Unterschied der Bahnen von zwei
benachbarten Anfangspunkten immer größer. Dies wirkt sich
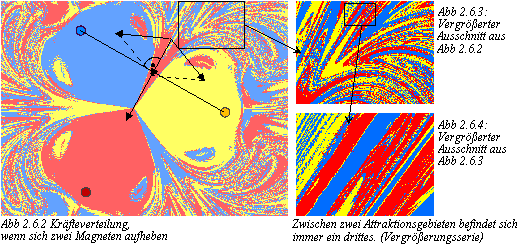
besonders an den Grenzen der Attraktionsgebiete(1)
aus: sie verzahnen sich stärker, und die Unvorhersagbarkeit nimmt zu.
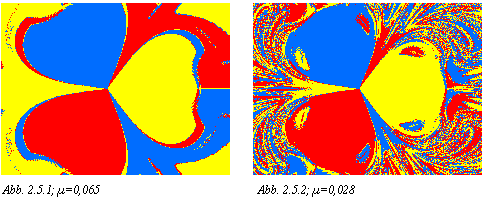
Die Abbildungen 2.5.1 und 2.5.2 verdeutlichen dies. Während bei einem
Wert von µ = 0,065 -außerhalb der eindeutigen Bereiche um die drei
Magneten- die Grenzen zwischen den Attraktionsgebieten noch relativ klar
sind, herrscht bereits bei einem Wert von µ = 0,028 ein chaotisches
Punktewirrwarr, bei dem kaum mehr von "Grenzen" im eigentlichen
Sinn des Wortes gesprochen werden kann. Auf den zweiten Blick lassen sich
jedoch Strukturen erkennen.
2.2 Versuchsdurchführung
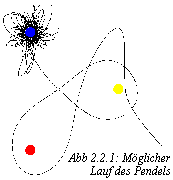 Bewegt man das Pendel zu einem beliebigen Anfangspunkt und läßt
ihm dann freien Lauf, so bewegt es sich in chaotischen Schleifen und kommt
schließlich (wegen der Luftreibung) über einem der drei Magneten
zum Stillstand. (Abb. 2.2.1)
Bewegt man das Pendel zu einem beliebigen Anfangspunkt und läßt
ihm dann freien Lauf, so bewegt es sich in chaotischen Schleifen und kommt
schließlich (wegen der Luftreibung) über einem der drei Magneten
zum Stillstand. (Abb. 2.2.1)
2.3 Theoretische Grundlagen der Simulation
[Dieser Punkt wurde hier weggelassen, weil er voll mit Formeln ist, die HTML
nicht darstellen kann. Wer sich dennoch dafür interessiert, der kann mir
gerne eine e-mail schicken.]
2.4 Optimierung der Formeln für die Simulation
[Dieser Punkt wurde hier weggelassen, weil er voll mit Formeln ist, die HTML
nicht darstellen kann. Wer sich dennoch dafür interessiert, der kann mir
gerne eine e-mail schicken.]
2.5 Veränderung der Ausgangsbedingungen
[Kleiner Ausschnitt gekürzt, ebenfalls wegen Formeln]
2.7 Verletzung der starken Kausalität
Versucht man, das Pendel mehrmals am gleichen Anfangspunkt zu starten, so könnte vermutet werden, daß das Pendel immer eine ähnliche Bahn beschreiben und schließlich beim selben Magneten hängenbleiben wird. Diese Vermutung beruht auf dem Axiom der starken Kausalität, das James C. Maxwell 1879 folgendermaßen beschrieb: "Es ist eine metaphysische Doktrin, daß gleiche Ursachen gleiche Wirkungen nach sich zögen. Niemand kann sie bestreiten. Ihr Nutzen aber ist gering in einer Welt wie dieser, in der gleiche Ursachen niemals wieder eintreten und nichts zum zweiten Mal geschieht. Das daran anlehnende physikalische Axiom [der starken Kausalität] lautet: Ähnliche Ursachen haben ähnliche Wirkungen. Dabei sind wir von der Gleichheit übergegangen zu Ähnlichkeit, von absoluter Genauigkeit zu mehr oder weniger grober Annäherung" (2)Bei chaotischen Systemen sieht die Wirklichkeit anders aus: Ähnliche
Anfangspunkte in einem "strittigen" Gebiet (also in einem Gebiet,
in dem die Grenzen der Attraktionsgebiete der einzelnen Magneten stark
verzahnt und flächenmäßig recht klein sind) führen zu
vollkommen verschiedenen Laufbahnen des Pendels. Die anfangs zwar
annähernd gleichen Anfangspunkte entfernen sich exponentiell voneinander
und enden meist bei verschiedenen Magneten. Dies ist der sogenannte
"Schmetterlingseffekt" oder, anders gesagt, die Verletzung der
starken Kausalität: In chaotischen Systemen können ähnliche
Ursachen völlig verschiedene Wirkungen haben; kleine (auf den ersten
Blick unbedeutende) Veränderungen können sich mit der Zeit derart
verstärken, daß sie nachher so groß wie die Meßwerte
selbst sind. Das Programm "MAUSPEND" demonstriert dieses Verhalten.
2.8 Anleitung zu den Simulationsprogrammen für das Magnetpendel
[Auch diesen Abschnitt habe ich weggelassen. Wer sich dennoch dafür
interessier (Programm oder Beschreibung), kann mir ja mal eine
e-mail schreiben...]
Zurück zum letzten Kapitel ("Deterministisches Chaos - allgemeine Vorbemerkungen")
Weiter mit dem nächsten Kapitel ("Das Drehpendel")
1 Das Attraktionsgebiet eines Magneten i ist (in diesem Fall) die Menge aller Anfangspunkte, deren (durch die Pendellaufbahn zugeordnete) Endpunkte über dem Magneten i liegen.
2 Worg [1], Seite 32
(C) Copyright 1997 by Johannes Schmid
letzte Änderung: 05. Januar 1997