Vorbem.
Magnetpend.
Drehpend.
Phänomene
Literatur
4. Chaotische Phänomene am Beispiel des Drehpedels
4.1 Bifurkationszenario
Bei einem relativ hohen M0 Brems (=0,105) tritt eine periodische Schwingung auf (Abb. 4.1.1). Bei einer Verkleinerung der Dämpfung ist eine höhere Schwingungsamplitude zu erwarten, da die Wirbelstrombremse weniger Energie abführt. Weil sich aber auch die Geschwindigkeit (und damit auch die Bremswirkung) des Pendels erhöht, wird die Amplitude nicht laufend höher, sondern pendelt sich bei einer gewissen (etwas größeren) Amplitude ein.Senkt man die Dämpfung (auf M0 Brems = 0,0994), so spaltet sich die Grundschwingung in zwei Schwingungen mit verschiedenen Amplituden auf, die sich nach jedem Schwingungsdurchgang abwechseln (Abb. 4.1.2). Dieses Verhalten nennt man Bifurkation, das sich wie folgt erklären läßt: "Die Eigenfrequenz des Pendels ist abhängig von der Amplitude (...). Da die Anregungsperiode [des Oszillators] konstant bleibt, liegt bei größerer Amplitude keine Resonanz vor und die Amplitude wird kleiner. Bei der kleineren Amplitude stimmen Eigenschwingperiode und Anregung wieder zusammen, es herrscht wieder Resonanz. Die Amplitude wächst und der Zyklus beginnt wieder von vorne."(1)
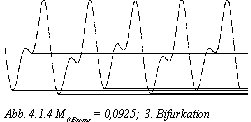
Verringert man die Dämpfung noch weiter (auf 0,093), so spaltet sich die Schwingung wiederum auf. Die beiden Teilschwingungen sind jetzt jeweils zwei Perioden lang. (2. Bifurkation, Abb. 4.1.3). Bei nochmaliger Verkleinerung von M0 Brems (auf 0,0925) teilt sich die Schwingung abermals in zwei Teilschwingungen mit jeweils vier verschiedenen Perioden auf. (3. Bifurkation, Abb. 4.1.4). Diese Schwingung wiederholt sich also erst nach dem achtfachen der ursprünglichen Periodenlänge. Ab hier sind die Abstände zwischen den Bifurkationen so klein, daß sie kaum mehr "getroffen" werden können.
Bei einem Wert von M0 Brems = 0,092 ist das Verhalten chaotisch. (Abb. 4.1.5) "Es stellt sich auch nach langer Einschwingzeit kein periodischer Vorgang ein, das System schwingt unregelmäßig (...). Der Vorgang ist natürlich immer noch deterministisch (...), aber nicht mehr stark kausal. Kleinste Störungen wirken sich stark auf das Verhalten aus, eine Langzeitvorhersage ist nicht mehr möglich (...)."(2)
Bei einer noch kleineren Dämpfung (M0 Brems = 0,06) tritt plötzlich wieder Ordnung auf - es stellt sich eine stabile Schwingung ein (Abb. 4.1.6). Diese nennt man ein "Fenster im Chaos".
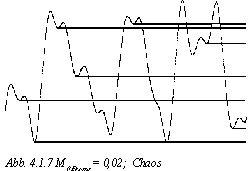
Verkleinert man M0 Brems weiter, werden die Schwingungen wieder chaotisch (Abb. 4.1.7).
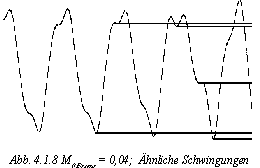
Betrachtet man eine Reihe von chaotischen Schwingungen in einer Folge, können mehrere ähnliche Schwingungen hintereinander erkannt werden, die schließlich "aufbrechen" und sich zu einer neuen Schwingung formieren (Abb. 4.1.8). Es handelt sich hierbei um das Phänomen der Unterbrechung [intermittency]. Hier bleibt ein physikalisches System einige Zeit statisch, bis es plötzlich für einige Zeit einen chaotischen Ausbruch zeigt und dann wieder statisch ist; danach kommt wieder ein chaotischer Ausbruch und so weiter.(3)
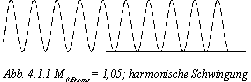
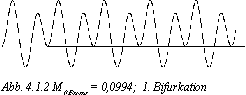
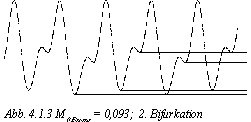
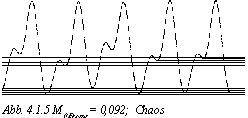

4.2 Poincaré-Schnitt
 Die Schwingung des chaotischen Drehpendels hat (neben den Konstanten)
genau drei Variablen, die den aktuellen Zustand des Pendels eindeutig
beschreiben. Diese Variablen sind die Auslenkung des Pendels j, dessen
Geschwindigkeit w und der Zustand des Oszillators, dem t modulo T(4)
entspricht, da die Anregung des Oszillators periodisch ist (d.h. sich alle T
Zeiteinheiten wiederholt). Sind alle Variablen exakt gegeben (in der
Realität aber niemals möglich), so kann die weitere Laufbahn des
Pendels berechnet werden.
Die Schwingung des chaotischen Drehpendels hat (neben den Konstanten)
genau drei Variablen, die den aktuellen Zustand des Pendels eindeutig
beschreiben. Diese Variablen sind die Auslenkung des Pendels j, dessen
Geschwindigkeit w und der Zustand des Oszillators, dem t modulo T(4)
entspricht, da die Anregung des Oszillators periodisch ist (d.h. sich alle T
Zeiteinheiten wiederholt). Sind alle Variablen exakt gegeben (in der
Realität aber niemals möglich), so kann die weitere Laufbahn des
Pendels berechnet werden.
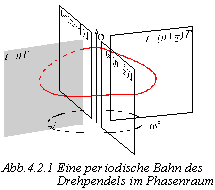
Die drei Variablen geben einen Raum, den sogenannten Phasenraum. In ihn kann die gesamte Bahn des Pendels eingezeichnet werden, indem für jede Phase des Pendels (bestimmt durch t modulo T, j und w) ein Punkt eingezeichnet wird. Der Raum wird des weiteren so gekrümmt, daß die Ebenen für t = nT (n element N0+) übereinanderliegen. Die Linien können sich nicht schneiden, da es sonst zu einem Punkt zwei Möglichkeiten geben würde, wie es vom Schnittpunkt aus weitergehen könnte, was aber unmöglich ist, da ein Punkt den Zustand des Pendels eineindeutig festlegen muß.
Die Bahn kann jedoch geschlossen sein. Das bedeutet dann, daß die
Schwingung des Pendels periodisch ist (sich wiederholt). In diesem Fall
handelt es sich um einen Bifurkationszustand und nicht um "echtes"
Chaos. "Ein charakteristisches Merkmal im Fall einer chaotischen
Bewegung ist, daß Kurven, die durch zwei benachbarte Punkte im
Phasenraum gehen, nicht beieinander bleiben, sondern sich exponentiell
voneinander entfernen."(5)

Da ein dreidimensionaler Raum schwer darzustellen und zu überblicken ist, reduziert man die Daten durch den Poincaré-Schnitt. Es wird hierbei eine günstig gelegte Ebene durch den Phasenraum gelegt und dann nur die Stoßpunkte durch die Ebene anstatt der gesamten Laufbahn des Pendels registriert. Eine günstige Schnittebene wird beispielsweise durch die Festlegung des Oszillators auf t modulo T = 0 erreicht.
Eine kontinuierliche Bahn wird also durch den Poincaré-Schnitt auf
eine Folge von Punkten reduziert, die man ihren Orbit nennt(6). Eine
periodische Bahn hat eine begrenzte Anzahl von Schnittpunkten, die gleich der
Zahl der Schwingungen des Pendels ist. Eine quasiperiodische Bahn (sie kommt
nicht zum Ausgangspunkt zurück, sondern ist geringfügig versetzt),
eine Bahn also, bei der sich alle Schwingungen ähneln, aber nicht gleich
sind, "produziert im Poincaré-Schnitt [eine] gepunktete Linie,
die das Zentrum des Bildes umschließt. (...) Während periodische
Bahnen im Poincaré-Schnitt als ein Muster aus isoliert liegenden
Punkten erscheinen, bilden quasiperiodische Orbits Linienstrukturen.
Chaotische Orbits hingegen füllen ganze Bereiche der Schnittebene aus
(...). Bilder von der Art (...) zeigen auf einen Blick, wo ein System sich
einfach, das heißt langfristig prognostizierbar, und wo es sich
chaotisch, das heißt auf lange Sicht unvorhersagbar,
verhält."(7)
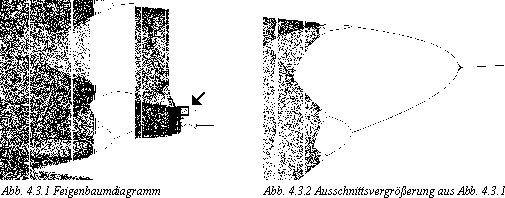
An der Abszisse der Abbildung 4.3.1 ist die Dämpfung (M0 Brems)
angetragen. Links beginnt sie bei 0 und endet rechts bei 0,125. An der
Ordinate ist die Auslenkung j der einzelnen Poincaré-Schnittpunkte
angetragen (oben ist +pi, unten -pi), die erst nach einer gewissen
Einschwingzeit des Pendels eingezeichnet wurden, da das Pendel eine bestimmte
Zeit braucht, bis es sich in der für die Dämpfung typischen
Schwingung befindet.
In der Vergrößerung lassen sich die Bifurkationsgrenzen ablesen
(die erste Bifurkation wurde nicht berücksichtigt, da der Wert der
Dämpfung nur sehr ungenau abzulesen ist):
4.3 Attraktoren
Wird die Bahn eines Systems nach einer gewissen Einschwingzeit in den
Phasenraum eingezeichnet, so nennt man das entstandene Gebilde einen
Attraktor. Wird das System mit verschiedenen Anfangswerten gestartet (z.B.
mit unterschiedlichen Anfangsauslenkungen j, aber bei gleichbleibenden
Konstanten wie etwa der Dämpfung), so nähert sich die Phasenbahn
dem Attraktor asymptotisch an. Es gibt verschiedene Arten von Attraktoren:
4.4 Feigenbaumdiagramm
Die Punkte des Poincaré-Schnitts eines Systems sind ausreichend, um
seinen Bifurkationsgrad und seine Komplexität bzw. Art (Bifurkation oder
Chaos) zu bestimmen. Ein System mit einer periodischen Schwingung hat genau
einen Schnittpunkt; nach der ersten Bifurkation genau zwei verschiedene
Schnittpunkte, nach der zweiten Bifurkation sind es vier. Dies liegt daran,
daß sich eine Schwingung mit n verschiedenen Schnittpunkten bei einer
Bifurkation in zwei verschiedene Schwingungen mit je n Schnittpunkten
aufteilt. Bei jedem Schritt verdoppelt sich also die Zahl der Schnittpunkte.
Das heißt, daß ihre Anzahl gleich 2^Grad der Bifurkation
[das "^" heißt "hoch" und ist fü die Browser,
die das nicht anders darstellen können] ist, oder umgeformt:
Grad = log2 Anzahl. Die
Anzahl der Schnittpunkte gibt somit die Komplexität einer Schwingung an.
Um dieses Phänomen näher zu untersuchen und um die Grenzen zwischen
den einzelnen Bifurkationen näher kennenzulernen, stellt man die
Pendelauslenkung j in den Schnittpunkten der Dämpfung M0 Brems
gegenüber (Abb 4.3.1).
| Bifurkationsgrad = i | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Dämpfung M0 Brems = ci | 0,09447 | 0,09277 | 0,09240 | 0,09232 | 0,09230 |
| Dämpfungsunterschied = ci-1 - ci | 0,00170 | 0,00037 | 0,00008 | 0,00002 | |
| Quotient d. Dämpfungsuntersch. | 4,6 | 4,6 | 4 |
Es fällt auf, daß der Quotient der Dämpfungsunterschiede (deltai = (ci-1 - ci) : (ci - ci+1) ) konstant ist. Die Abweichung des letzten Wertes (delta5) ist auf die begrenzte Genauigkeit der Meßwerte zurückzuführen. Die Bifurkationsgrenzen lassen sich also folgendermaßen berechnen: ci = cunendl. + k · delta-i, wobei in diesem Fall cunendl. ungefähr 0,0922976 und k ungefähr 0,0459662 ist.
Das chaotische Punktewirrwarr ist also keine Schwingung mit relativ hohem
Bifurkationsgrad (wie man vielleicht annehmen könnte), da Schwingungen
mit endlichem Bifurkationsgrad nur bei einer Dämpfung auftreten, die
größer als cunendl. ist.
Diese Datenreduktion (= Diskretierung) wird nun auch für die
Erzeugung der Daten verwendet. Das System des Rotationspendels kann somit
nicht mehr angewandt werden, sondern es wird ein System benötigt, das
bei jedem Iterationsschritt verwendbare, d.h. sinnvolle Daten liefert: die
logistische Funktion. Sie ist eine einfache mathematische Abbildung und hat
auf den ersten Blick nichts mit den bereits behandelten Pendelschwingungen zu
tun.(9)
(4.5.1) Xneu = c · Xalt · (1 - Xalt)
X ist hierbei die Darstellungsvariable, c der Kontrollparameter. Diese
iterative Abbildung liefert zu jedem Wert einen neuen, von c abhängenden
Wert. Dieser kann dann erneut als "alter" Wert in die Gleichung
eingesetzt werden.
"Die logistische Abbildung wird im Einheitsintervall x element [0;1]
betrachtet. In diesem Einheitsintervall besitzt sie die Nullstellen xz1 = 1
und xz2 = 0. Ihr Maximum erhält man aus der Differentiation von (4.5.1)
zu xmax = 0,5. Der dazugehörige Funktionswert ist
f(xmax) = [c] : 4. Wegen der
Bedingung x element [0;1] ist also [c] element [0;4]."(10)
Zahlenreihen, die durch die logistische Iterationsfunktion gewonnen wurden
(wobei der Anfangswert gleichgültig ist, sofern er ungleich 0 und ungleich 1 ist, da
sonst Xneu ebenfalls Null ist), können in drei grundsätzlich
verschiedene Arten untergliedert werden:
Betrachtet man die periodischen Schwingungen (Abb. 4.4.2 bis 4.4.4)
genauer, so erinnern sie stark an ein Bifurkationsszenario, wie es in 4.1
besprochen wurde (eine Schwingung spaltet sich bei jeder Bifurkation in zwei
Unterschwingungen auf).
Die Abbildungen 4.4.7 bis 4.4.10 zeigen verschiedene Ausschnitte und
Vergrößerungen aus dem Feigenbaumdiagramm der logistischen
Funktion. Der Kontrollparameter c wurde an der Abszisse angetragen (von 2,5
bis 4) und von links nach rechts schrittweise erhöht. Die jeweils
vorkommenden Funktionswerte X wurden (nach einer gewissen
"Einschwingzeit" von 100 Iterationen) auf der Ordinate angetragen.
Untersucht man bei der logistischen Funktion (genauso wie beim Drehpendel)
die Verhältnisse zwischen den Aufspaltungspunkten, so stößt
man auf ein interessantes Ergebnis:
4.5 Logistische Funktion
Das Rotationspendel ist ein sich kontinuierlich entwickelndes bzw. in der
Simulation ein sich annähernd kontinuierlich entwickelndes
physikalisches System. Das heißt, daß sich die beobachtete
Variable (= Darstellungsvariable, im behandelten Fall die momentane
Auslenkung j) kontinuierlich ändert, d.h. größer und kleiner
wird. Zur Analyse des Systems wird eine Datenreduktion vorgenommen: Es werden
nur noch die Tiefpunkte der Auslenkung registriert, der Rest der
Pendellaufbahn wird nicht beachtet.


| Bifurkationsgrad = i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Kontrollparameter ci | 3,00088 | 3,44816 | 3,54385 | 3,56434 | 3,56873 | 3,56967 |
| Parameterdifferenz ci - ci-1 | 0,44728 | 0,09569 | 0,02049 | 0,00439 | 0,00094 | |
| Quotient d. Parameterdifferenz | 4,67 | 4,67 | 4,67 | 4,67 |
Auch hier ist der Quotient der Kontrollparameterdifferenzen delta konstant. Ein genauerer Wert lautet(11): delta = 4,6692. Die Bifurkationsgrenzen lassen sich ebenso wie beim Drehpendel berechnen:
(4.5.2) ci = cunendl. + k · delta-i ist ungefähr 3,56992 - 2,65699 · 4,6692-i
delta wird auch Feigenbaumkonstante genannt. Sie wird als universell bezeichnet, da sie nicht nur für die Gleichung (4.5.1) gilt, sondern auch für alle Gleichungen, die ein quadratisches Maximum haben. Hier einige Beispiele(12):
(4.5.3)  (cmax = 1)
(cmax = 1)
(4.5.4) 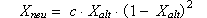 (cmax = 6,75)
(cmax = 6,75)
(4.5.5)  (cmax = 2)
(cmax = 2)
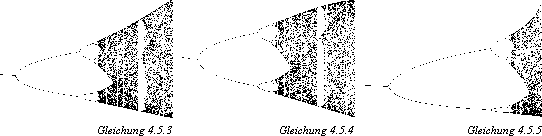
Das Phänomen des Feigenbaumdiagramms und der Feigenbaumkonstante d tritt übrigens bei allen oder zumindest bei den meisten deterministisch chaotischen Systemen auf. Deterministisches Chaos ist also nicht etwas rein Chaotisches und vollkommen Unvorhersagbares, sondern verhält sich in gewissen Punkten gewissermaßen geregelt. Die Regeln sind zwar nicht der Art, wie man sie aus der klassischen Physik kennt, lassen es aber trotzdem zu, gewisse Aussagen über ein System zu treffen und gewisse Parallelen zu anderen Systemen zu ziehen.
Zurück zum letzten Kapitel ("Das Drehpendel")
Weiter mit dem Literaturverzeichnis
1 Worg [1], Seite 49
2 Worg [1], Seite 49
3 Lundquist, March, Tosi [2], Seite 20f
4 t modulo T := Rest von der Teilung von t durch T, d.h.: t-[t/T]
5 vgl. Worg [1], Seite 17
6 vgl. Breuer [5], Seite 33
7 Breuer [5], Seite 33
8 vgl. Lundquist, March, Tosi [2], Seite 21
9 vgl. Worg [1], Seite 63
10 Atmanspacher, Morfill [3], Seite 25
11 aus Worg [1], Seite 66
12 aus Worg [1], Seite 67
(C) Copyright 1997 by Johannes Schmid
letzte Änderung: 05. Januar 1997